No.33 ゾンビ島 (Zombie Island)

時間制限:$2.0sec$ / メモリ制限:$256MB$

問題文

JOI 君が住んでいる島がゾンビに侵略されてしまった．JOI 君は島で一番安全な避難場所として設定されているシェルターに逃げ込むことにした．

JOI 君が住んでいる島は町 1 から町 N までの N 個の町からなり，町と町とは道路で結ばれている．島には M 本の道路があり，すべての道路は異なる 2 つの町を結んでいる．JOI 君は道路を双方向に自由に移動できるが，道路以外を通って町から別の町に行くことはできない．

いくつかの町はゾンビに支配されており，訪れることが出来ない．ゾンビに支配されている町から S 本以下の道路を使って到達できる町を危険な町という．それ以外の町を危険でない町という．

JOI 君の家は町 1 にあり，避難先のシェルターは町 N にある．町 1，町 N はゾンビに支配されていない．島の道路は移動するのに時間がかかるので，JOI 君は町を移動するたびに，移動先の町で一晩宿泊しなければならない．JOI 君は，危険でない町で宿泊する場合は宿泊費が P 円の安い宿に泊まるが，危険な町で宿泊する場合はセキュリティのサービスが優良な宿泊費が Q 円の高級宿に泊まる．JOI 君はできるだけ宿泊費が安くなるように移動して，町 N まで避難したい．町 1 や町 N では宿泊する必要はない．

JOI 君が 町 1 から町 N まで移動するときに必要な宿泊費の合計の最小値を求めよ．

入力

入力は 2 + K + M 行からなる．

1 行目には，4 つの整数 N, M, K, S (2 ≦ N ≦ 100000, 1 ≦ M ≦ 200000, 0 ≦ K ≦ N - 2, 0 ≦ S ≦ 100000) が空白を区切りとして書かれている．これは，島が N 個の町と M 本の道路からなり，N 個の町のうち K 個の町がゾンビに支配されており，ゾンビに支配されている町から S 本以下の道路を使って到達できる町を危険な町と呼ぶことを表す．

2 行目には，2 つの整数 P, Q (1 ≦ P ＜ Q ≦ 100000) が空白を区切りとして書かれている．これは，JOI 君が危険でない町では宿泊費が P 円の宿に泊まり，危険な町では宿泊費が Q 円の宿に泊まることを表す．

続く K 行のうちの i 行目 (1 ≦ i ≦ K) には，整数 Ci (2 ≦ Ci ≦ N - 1) が書かれている．これは，町 Ci がゾンビに支配されていることを表す．C1, ..., CK は全て異なる．

続く M 行のうちの j 行目 (1 ≦ j ≦ M) には，2 つの整数 Aj, Bj (1 ≦ Aj ＜ Bj ≦ N) が空白を区切りとして書かれている．これは，町 Aj と町 Bj との間に道路が存在することを表す．同じ (Aj, Bj) の組が 2 回以上書かれていることはない．

与えられる入力データにおいては，町 1 から町 N までゾンビに支配されていない町のみを通って移動できることが保証されている．

出力

JOI 君が町 1 から町 N まで移動するときに必要な宿泊費の合計の最小値を 1 行で出力せよ．

出力が 32 ビット符号付き整数の範囲に収まるとは限らないことに注意せよ．

入出力例

13 21 1 1
1000 6000
7
1 2
3 7
2 4
5 8
8 9
2 5
3 4
4 7
9 10
10 11
5 9
7 12
3 6
4 5
1 3
11 12
6 7
8 11
6 13
7 8
12 13

11000

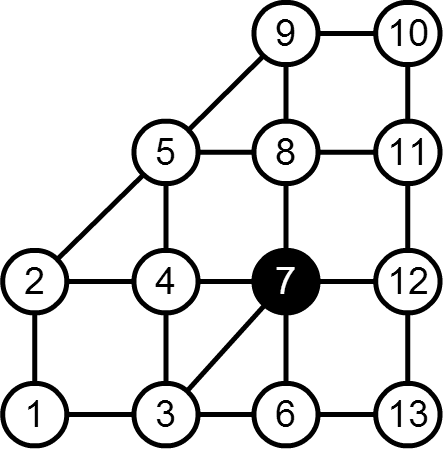
入出力例 1 は，以下の図に対応している．円は町を，線は道路を表す．

この場合，町 3，町 4，町 6，町 8，町 12 が危険な町である．

以下のような順番で町を移動すると，宿泊費の合計を最小にできる．

• 町 1 から町 2 に行く．町 2 で宿泊費が 1000 円の安い宿に宿泊する．
• 町 2 から町 5 に行く．町 5 で宿泊費が 1000 円の安い宿に宿泊する．
• 町 5 から町 9 に行く．町 9 で宿泊費が 1000 円の安い宿に宿泊する．
• 町 9 から町 10 に行く．町 10 で宿泊費が 1000 円の安い宿に宿泊する．
• 町 10 から町 11 に行く．町 11 で宿泊費が 1000 円の安い宿に宿泊する．
• 町 11 から町 12 に行く．町 12 で宿泊費が 6000 円の高級宿に宿泊する．
• 町 12 から町 13 に行く．町 13 では宿泊しない．

JOI 君がこのような経路で移動したとき，宿泊費の合計は 11000 円になるので，11000 を出力する．

21 26 2 2
1000 2000
5
16
1 2
1 3
1 10
2 5
3 4
4 6
5 8
6 7
7 9
8 10
9 10
9 11
11 13
12 13
12 15
13 14
13 16
14 17
15 16
15 18
16 17
16 19
17 20
18 19
19 20
19 21

15000